三年前，我们聊过一些与 HDR 图像显示及其 Web 传播方式相关的内容，时至今日，HDR 在图像领域终于有了一些确定的标准与实践。今年，W3C 发布了 PNG 3.0 标准，正式支持了 HDR，这也是时隔 22 年 PNG 再次迎来标准更新。

借此契机，我们可以把这个话题捡起来。这篇文字重新梳理了以下 HDR 图像显示相关的基础知识与最新进展。

定义颜色

在购买显示器、投影仪、相机或打印机等与色彩有关的设备，或观看相关评测时，可能会看到这样一张图。

这张图称为 CIE 1931 色度图（CIE 1931 Chromaticity Diagram），也常被称为马蹄图或舌形图。这张图及其代表的色彩空间会在后文中多次提及。为了理解它的含义，我们首先来聊一聊它所诞生的历史和背景。

三色理论

1666 年，牛爵爷 Isaac Newton 通过三棱镜将太阳光分解为不同颜色的连续可见光谱，并通过重新混合还原白色光，证明了白色光不是一种纯色光，而是由多种不同颜色的光混合而成。1704 年，其著作《光学》（Opticks）问世，为色彩科学领域奠定了基础。

Isaac Newton 的三棱镜分光实验。

1802 年，英国医生 Thomas Young 进行了假设，人眼中存在三种不同类型的光感受器，每种感受器只对可见光谱中的特定频率敏感，三种感受器对光的混合反应产生了实际的颜色知觉。1860 年，德国物理学家 Hermann von Helmholtz 对该理论进行了进一步发展，明确了感受器并非仅对单一频率的可见光有反应，每种感受器均对光谱所有频率有所反应，区别在于，每种感受器对不同频率的敏感程度不同。同时，通过不同光波长与视网膜的对照实验，确定视网膜内的感受器分为短波敏感（紫色）、中波敏感（绿色）、长波敏感（红色）三种类型。此理论被称为杨 · 亥姆霍兹理论（Young–Helmholtz Theory），又称三色理论（Trichromatic Theory）。1980 年，英国生物学家 J. K. Bowmaker 与 H. J. Dartnall 证实了对应的三种视网膜锥状细胞，并确定对应的敏感波段为 L 型细胞约 564-580 nm、M 型细胞约 534-545 nm、S 型细胞约 420-440 nm，为三色理论提供了生理学证据。

1854 年，德国物理学家 Hermann Günther Graßmann 在大量光混合实验的基础上，总结出以下四条规律，称为格拉斯曼定律（Grassmann’s Laws）：

  • 人眼能且只能感受颜色的三种特性：色相、饱和度与亮度。
  • 当两种色光混合时，如果其中一种发生了变化，混合结果也会随之变化。
  • 色彩表现一致的两种光，无论其混合构成是否一致，当这两种光参与混合时，它们对混合效果的作用都是一致的。
  • 混合光的总亮度等于参与混合的光的颜色之和。该规律同样于 1909 年由英国天文学家 William de Wiveleslie Abney 提出，亦称阿伯尼定律（Abney’s Law）。

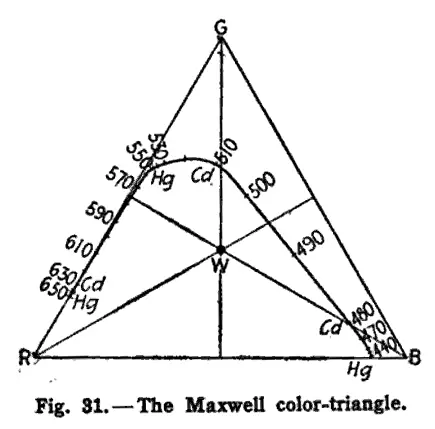
1855 年，知名物理学大佬 James Clerk Maxwell 基于其建立的颜色方程，通过红、绿、蓝三种基色作为等边三角形的顶点，提出了著名的颜色三角形，其内部任意一点到三遍的距离表示三种基色混合的相对比例，而三角形中心表示白点。

麦克斯韦颜色三角。

1861 年，J. C. Maxwell 在苏格兰皇家学院展出了一张使用三色曝光合成的照片，内容是一个苏格兰花格缎带。这是世界上第一张彩色照片。

颜色匹配实验

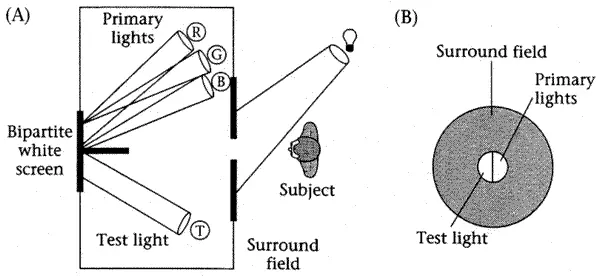
在 20 世纪 20 年代，为了进一步了解三色理论，也为了更加准确地量化颜色，科学家们设计了如下的颜色匹配实验：

  • 用一块隔板将一块纯色光屏分隔为两个部分。
  • 隔板一侧使用待测的单色光源照亮光屏，这一侧称为参考域（Reference Field）。
  • 隔板另一侧使用红、绿、蓝三种基色混合照亮光屏，这一侧称为匹配域（Matched Field）。
  • 将一块圆孔隔板放置在观察者与光屏之间，圆孔面积被隔板分隔，且足够小到受试者观察光屏的视场角为 2°，以此保证光屏投射的光线大致落在观察者视网膜的中央凹附近。
  • 实验时，在设定参考域颜色与亮度后，调节匹配域三种基色的亮度，直到观察者确认匹配域与参考域的颜色一致，通过圆孔的光形成一个完整的纯色圆形，以此测算参考域测试光源颜色对应的三种基色的混合比例。

颜色匹配实验示意图。

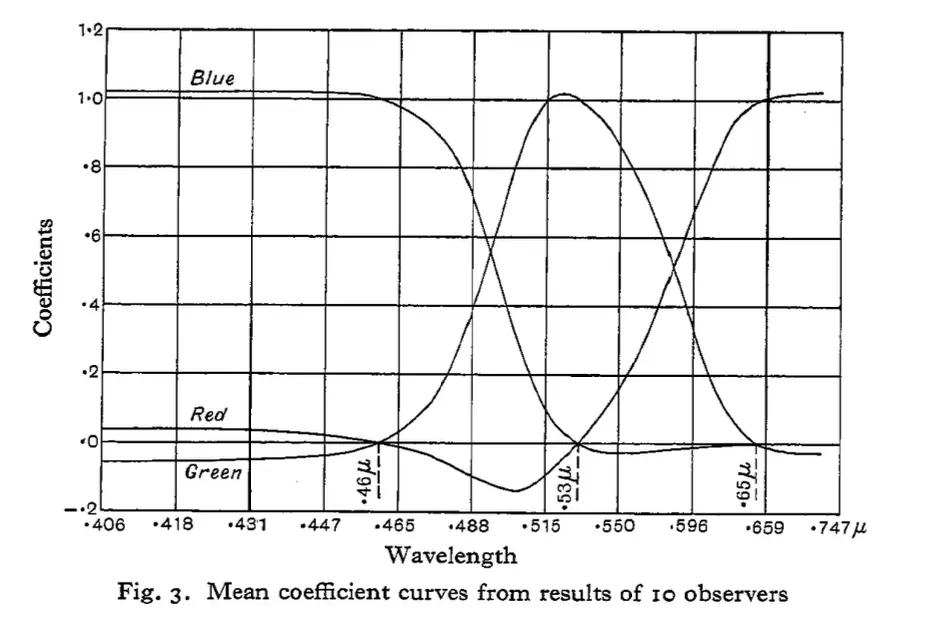
1928 年，英国物理学家 William David Wright 通过 650 nm（红）、530 nm（绿）、460 nm（蓝）三个频率的基色，邀请 10 名观察者参与实验，得到以下实验数据。

1928 年，W. D. Wright 实验所得的颜色匹配函数。

1931 年，英国物理学家 John Guild 通过 700 nm（红）、546.1 nm（绿）、435.8 nm（蓝）三个频率的基色，邀请 7 名观察者参与实验，得到以下实验数据。

1931 年，J. Guild 实验所得的颜色匹配函数。

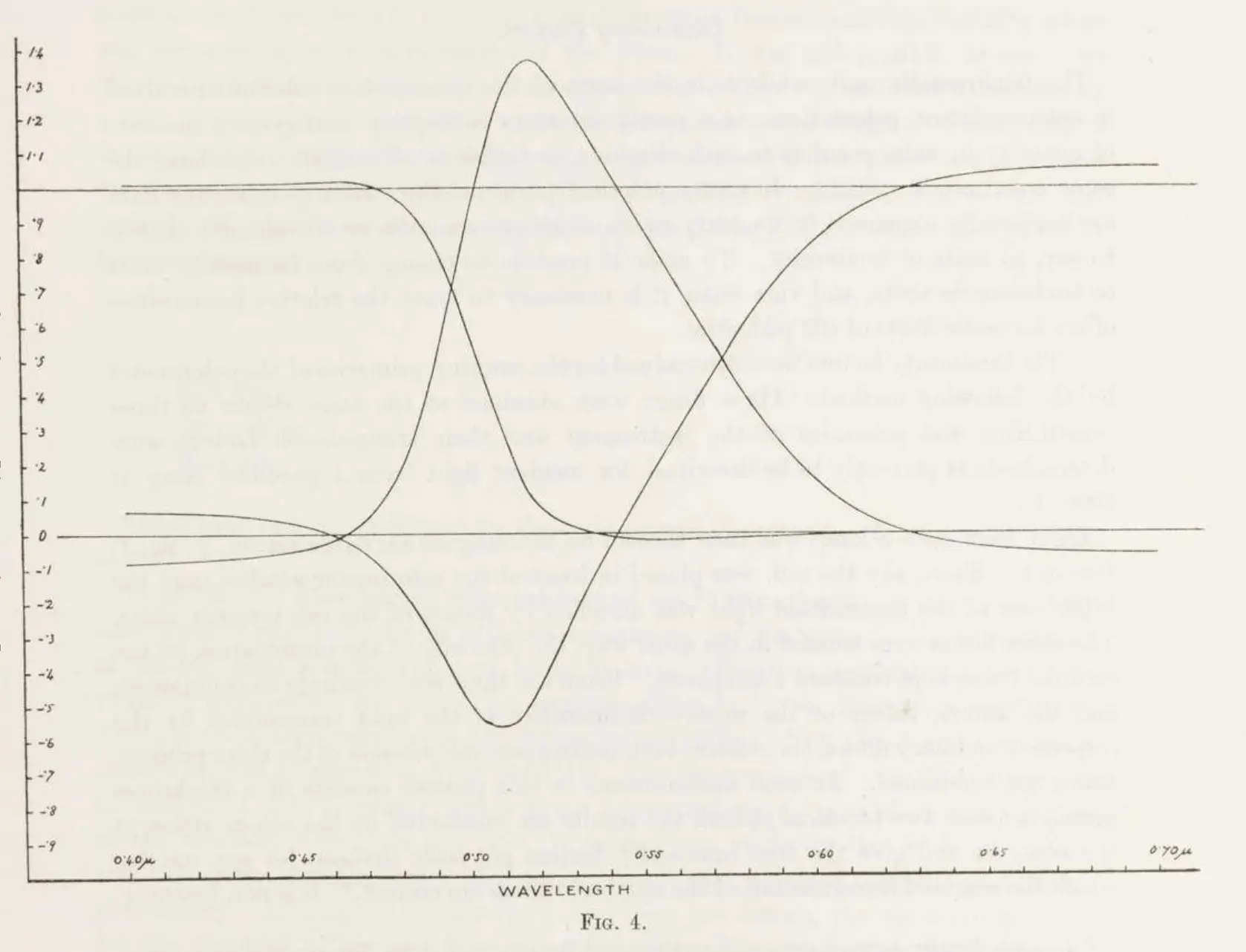
同样在 1931 年，国际照明委员会（Commission internationale de l’éclairage，CIE）通过整理上述两项实验的数据，确定以 700 nm（红）、546.1 nm（绿）、435.8 nm（蓝）三个频率的光作为基色，并通过照度比率 1 : 4.5907 : 0.0601 与辐射功率 72.0962 : 1.3791 : 1 对三种基色的单位进行了规范化，最终整理出以下的 CIE 1931 RGB 颜色匹配函数。其中，横坐标表示目标颜色的频率，纵坐标表示各个基色规范化后的亮度值。

CIE 1931 RGB 颜色匹配函数

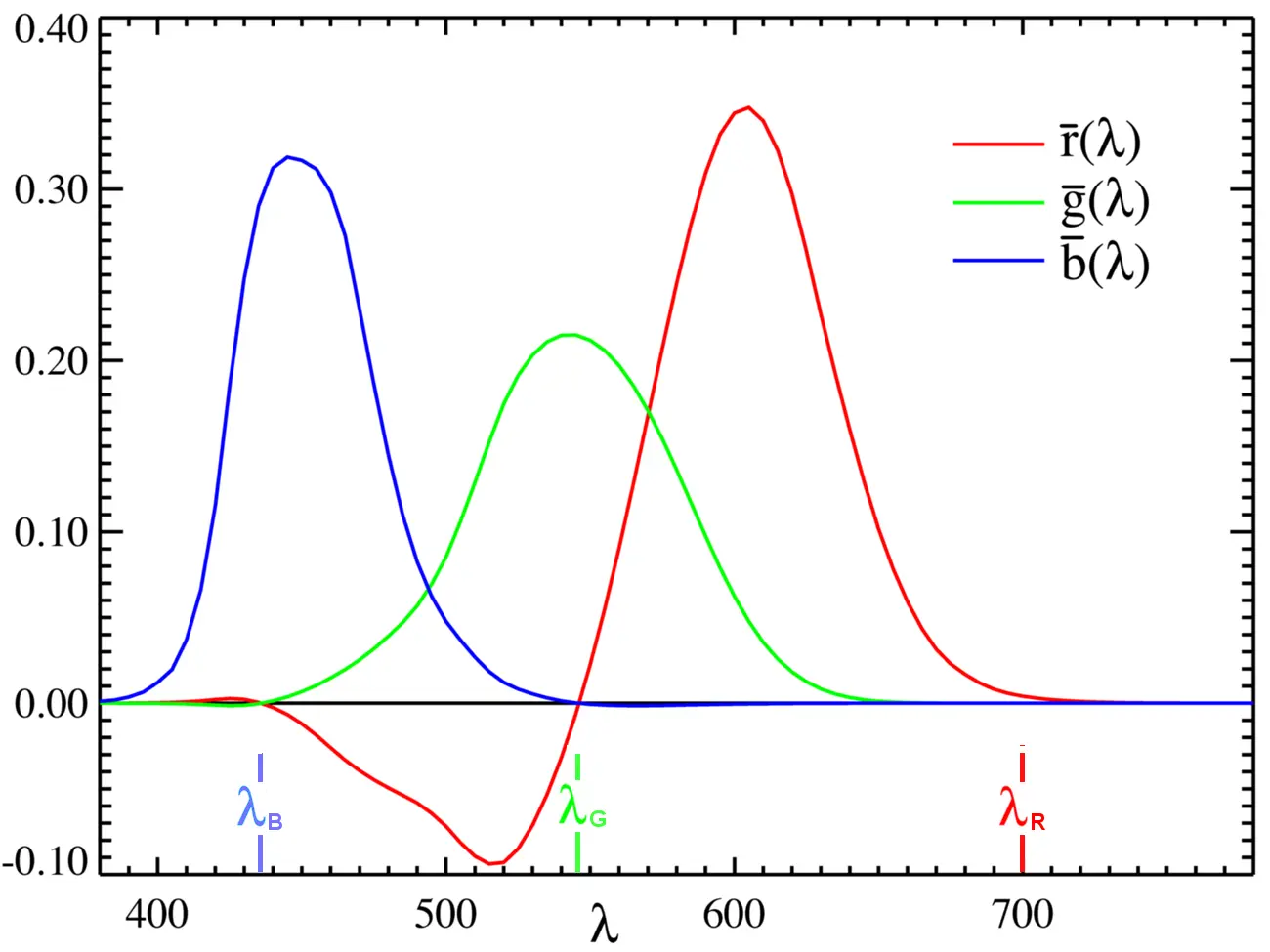
在 20 世纪初，汞蒸气灯是实验室标准且成熟的光源，435.8 nm 与 546.1 nm 是汞元素的特征谱线，纯度高且获取方便稳定。

受当时的技术条件限制，实验环境难以精确分离单个波长的光，选择 700 nm 作为基色频率之一，是因为人眼在这个波长下的感知相对稳定，当基色波长产生少量误差时对实验结果的影响极小。

构建色度图

在颜色匹配实验的部分，你可能会发现数据图表里一个奇怪的现象，为什么会有些频率的光，会有对应基色光的亮度存在负值？难道还能发出负亮度的光吗？

这是因为，实验者们发现，存在一些频率的可见光，无论如何调整匹配域中三基色的占比，都无法实现匹配。因此，实验者们在参照域中补充基色以完成匹配，在这种情况下，等价于匹配域基色减去对应的量。

为了便于色彩标准的理解和使用，CIE 决定重新定义颜色匹配函数的三种构成，使每种频率对应的三种混合构成均不为负数。于是他们捣鼓出了一个矩阵，通过对原本三种基色进行线性计算，将原本的 RGB 颜色空间映射为由三个不存在于物理世界的颜色构成的 XYZ 色彩空间。

\[\begin{bmatrix}X \\ Y \\ Z\end{bmatrix} = \frac{1}{0.17697}\begin{bmatrix}0.49 & 0.31 & 0.20 \\ 0.17697 & 0.81240 & 0.01063 \\ 0.00 & 0.01 & 0.99\end{bmatrix}\begin{bmatrix}R \\ G \\ B\end{bmatrix}\]

经过转换后，可以得到以下的颜色匹配函数。

CIE 1931 XYZ 颜色匹配函数

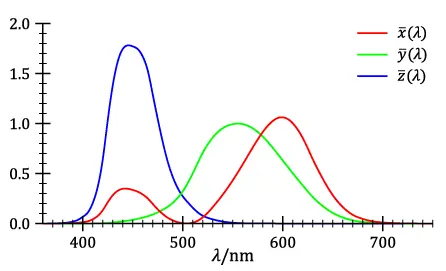
如果将 XYZ 三种构成作为一个三维坐标系的三个坐标轴，那么我们将各个频率可见光作为颜色向量，构成如下图表。

经过转换后的三维坐标图

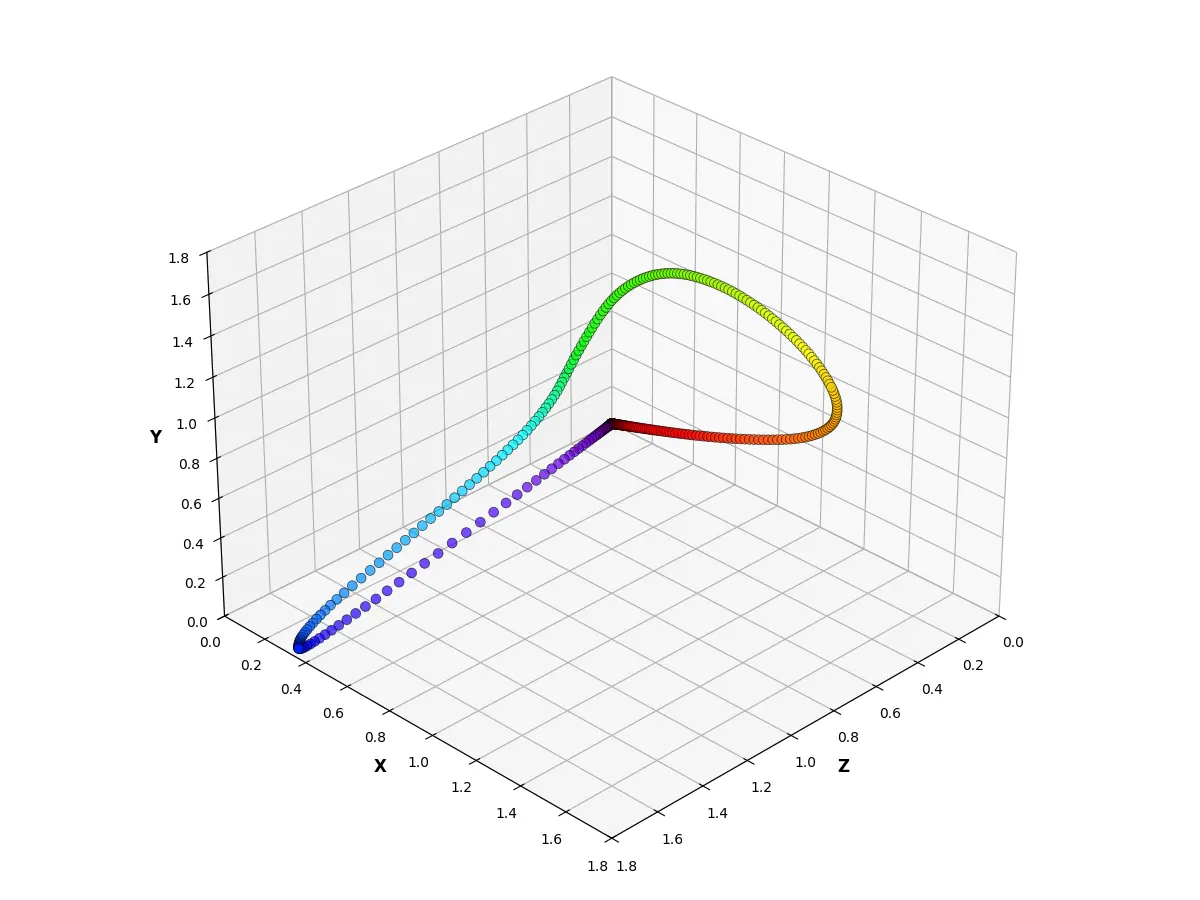
根据格拉斯曼定律，光的亮度可以进行线性计算。如果忽略亮度信息，则可以在这个三维坐标系中创建一个 \(X + Y + Z = N\)（\(N\) 为常量）的平面，这个平面上的所有点亮度都是一致的。为方便量化，我们选择 \(X + Y + Z = 1\) 的平面，称为等亮度平面，并将各个点的颜色向量归一化到这个平面上，此时我们可以获得如下图表。

将数据归一化到等亮度平面后的三维坐标图

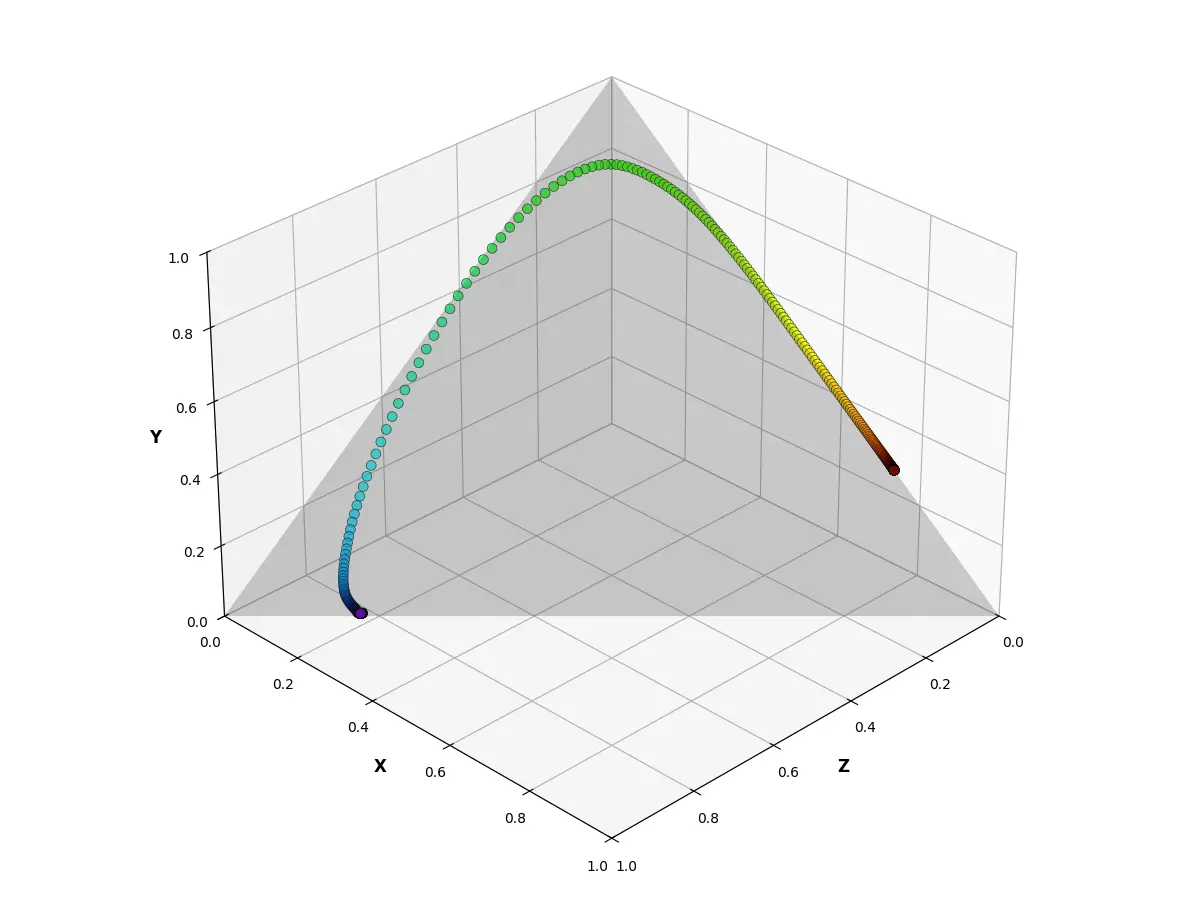
由于 \(X + Y + Z = 1\)，因此可以省略 Z 轴的信息，将等亮度平面投影到 X-Y 平面上，得到如下图表。

投影到 X-Y 平面后的三维坐标图

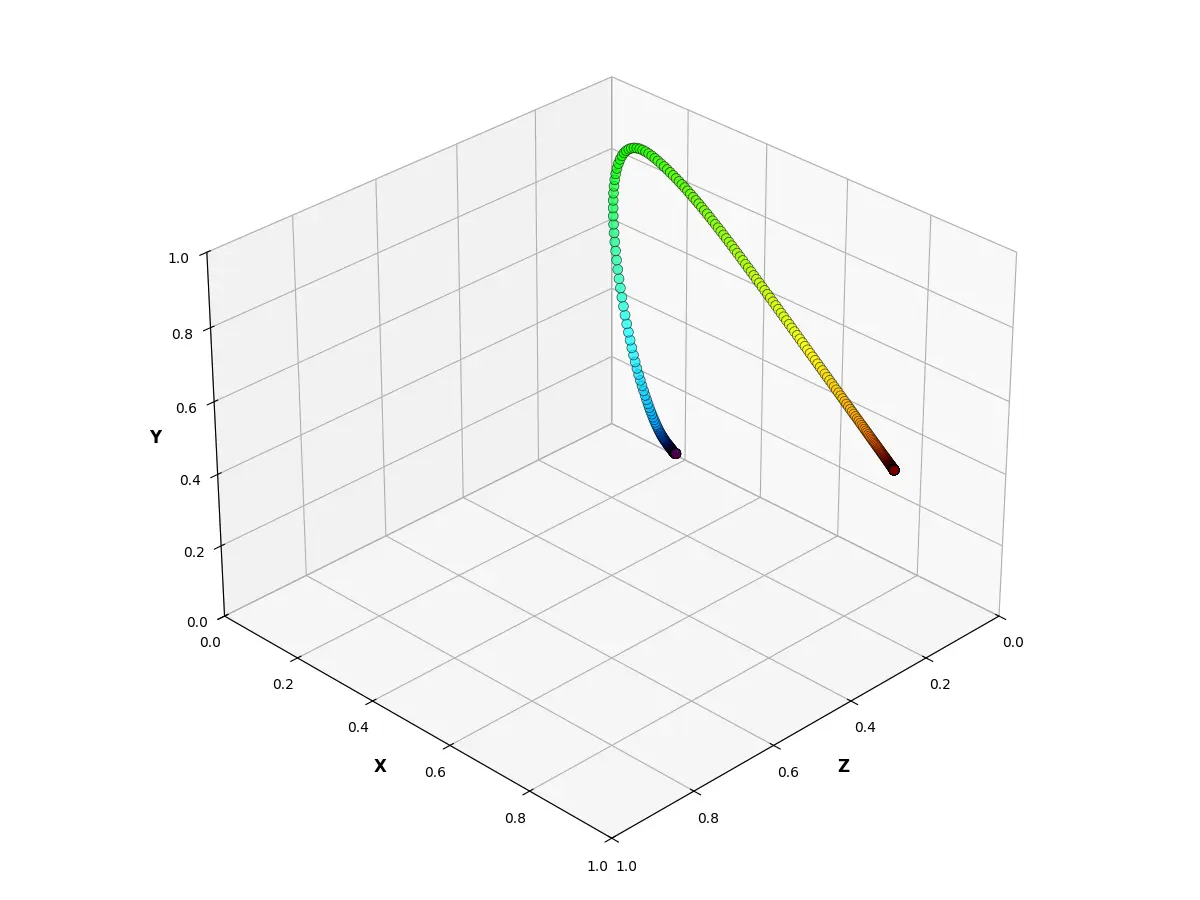
将三维坐标系简化为 X-Y 二维坐标系之后，是不是很眼熟？这些光谱颜色构成的曲线就是 CIE 1931 色度图中上方的那一条曲线，称为光谱轨迹（Spectral Locus）。当光谱轨迹上任意两点之间进行连线时，连线上的所有点均表示这两种颜色的混合色，这些线填充后的平面区域代表了人眼可见的所有颜色，这就是我们在开头所看到的 CIE 1931 色度图。

色彩空间

CIE 1931 色度图所描述的色彩空间是一个设备无关色彩空间（Device-Independent Color Space），它包含了所有人眼可见的颜色，因此也会经常被用作其它色彩空间的参照标准。

对于计算机图形学领域，大部分色彩空间基于 RGB 色彩模型进行构建，这些色彩空间通常包含以下三个部分：色彩原色、白点与转换函数。

色彩原色

色彩原色（Color Primaries）定义了一个基于 RGB 色彩模型的色彩空间所使用的三种基色，以最常见的 sRGB 色彩空间为例，在 CIE 1931 色度图中，三个基色的坐标分别为红色 (0.64, 0.33)、绿色 (0.30, 0.60) 与蓝色 (0.15, 0.06)。

由于 RGB 色彩模型的特性，当在 CIE 1931 色度图中将三个基色所代表的点进行连接时，所形成的这个三角形就代表了 sRGB 这个色彩空间内所能表示的所有颜色（不考虑亮度）。一个色彩空间所能表现的颜色范围也被称为这个色彩空间的色域（Gamut），刚才所围成的三角形，就是色域在等亮度平面上的投影。

sRGB 在 CIE 1931 色度图中的表示

这是不同色彩空间的色彩原色在 CIE 1931 色度图中的坐标位置：

  • sRGB / Rec. 709: (0.64, 0.33), (0.30, 0.60), (0.15, 0.06)
  • Adobe RGB: (0.64, 0.33), (0.21, 0.71), (0.15, 0.06)
  • DCI-P3 / Display P3: (0.68, 0.32), (0.265, 0.69), (0.15, 0.06)
  • Rec. 2020 / Rec. 2100: (0.708, 0.292), (0.170, 0.797), (0.131, 0.046)

白点

白点（White Point）是 RGB 色彩模型的色彩空间中，三种基色均使用最大值进行混合时所获得的颜色，它代表了色彩空间三种基色最大值之间的比例关系。

与色彩原色一样，白点一般在 CIE 1931 色度图中以等亮度平面的投影进行表示。sRGB 的白点坐标为 (0.3127, 0.3290)，是 CIE 所定义的标准光源颜色之一，色温约为 6500K，代表平均日光颜色，被称为 D65。

色温是表示光源光色的物理量，在色彩科学中通常也用于表示白色点的颜色属性。

在热力学中，黑体（Black Body）是一种能吸收所有外来电磁辐射的理想物体，不存在任何反射与透射。黑体所辐射出的电磁波被称为黑体辐射，随着温度升高，黑体辐射的光谱分布也会发生变化。

通常采用热力学温度的值（单位为 Kelvin，符号为 K，0K = -273.15°C）作为对应黑体辐射光色的色温值。

这是不同色彩空间的白点在 CIE 1931 色度图中的坐标位置：

  • sRGB / Rec. 709 / Adobe RGB / Display P3 / Rec. 2020 / Rec. 2100: (0.3127, 0.3290)
  • DCI-P3: (0.314, 0.351)

除此之外，一些色彩空间明确定义了白点亮度（White Point Luminance），比如 sRGB 的白点亮度为 80 cd/m²（另一个常见的单位表示是 nit，nit 等同于 cd/m²）。然而，绝大部分日常使用的设备都会根据设备的实际能力来调整白点亮度，在很多人的使用习惯里，80 cd/m² 是一个暗得没眼看的水平，现在大部分的显示设备都已经能完整覆盖许多色彩空间的亮度范围，因此，非严谨地，在通常的讨论里，讨论色域只是在讨论色彩原点与白点的色度坐标。比如一个使用 sRGB 色彩原色与白点坐标的显示器，能显示大于 80 cd/m² 的亮度，那么它色彩空间的色域必然能 100% 覆盖 sRGB 色彩空间的色域。

这是一些常见的色彩空间定义的白点亮度：

  • sRGB / Display P3：80 cd/m²
  • Rec. 709：100 cd/m²
  • Adobe RGB：160 cd/m²
  • DCI-P3：48 cd/m²

转换函数

转换函数（Transfer Function）定义了色彩空间中数值与实际亮度之间的映射关系。

在计算机领域，连续的亮度值通常被量化为离散的整型数据进行存储与处理，这些整数所能表现的亮度数量是有限的。以一个 8bit 的整型表示由黑到白的单色亮度变化为例，它所能记录的值范围为 0-255，只能表示 256 种亮度。那么，将 0 映射为黑色，255 映射为白色，用中间的值表示不同的灰色，直接将这些整数等间隔地映射为对应等间隔的亮度值，是不是就可以了？

答案是否定的，因为人眼对亮度的感知并不是线性的，与高亮度的变化相比，人眼对低亮度的变化更为敏感。如果通过线性映射来表示亮度变化，那么低亮度区域用来表示亮度的整数数量会非常有限，而高亮度区域会浪费大量的整数。

19 世纪，德国实验心理学家 Ernst Heinrich Weber 与 Gustav Theodor Fechner 发现，人类对刺激强度的感知变化与实际刺激强度之间存在对数关系，这一现象被称为韦伯 · 费希纳定律（Weber–Fechner Law），而后，美国物理学家 Stanley Smith Stevens 通过实验发现，人类对刺激强度的感知变化与实际刺激强度之间存在幂函数关系，这一现象被称为斯蒂文斯定律（Stevens’ Power Law）。

为了对人眼的非线性感知进行补偿，大部分色彩空间会采用非线性的函数作为转换函数，而最常见的转换函数类型是伽马校正（Gamma Correction），一般简称为伽马（Gamma），它的数学表达式如下：

\[L = {\alpha}V^{\gamma}\]

其中 \({\alpha}\) 为峰值亮度，而 \({\gamma}\) 作为幂指数，决定了输入（\(V\)，信号数值，取值为 \([0, 1]\)）与输出（\(L\)，实际亮度，单位 cd/m²，取值为 \([0, {\alpha}]\)）之间的非线性关系。

除了伽马之外，一些色彩空间也使用了其它类型的转换函数，一些用于 HDR 的色彩空间所使用的转换函数会在后文介绍。

这是不同色彩空间使用的转换函数：

  • sRGB / Adobe RGB / Display P3：Gamma 2.2（γ = 2.2）
  • Rec. 709 / Rec. 2020 ：Gamma 2.4（γ = 2.4）
  • DCI-P3：Gamma 2.6（γ = 2.6）
  • Rec. 2100：PQ / HLG

上述的公式是信号到亮度的转换函数，比如图像或视频的信号数值映射到显示设备，称为电光转换函数（Electro-Optical Transfer Function，EOTF）。与之对应的，亮度到信号的转换函数称为光电转换函数（Opto-Electrical Transfer Function，OETF），其幂函数的幂值为 γ 的倒数。

实际上，上述这些色彩空间所使用的转换函数也不是真正的 Gamma 函数，而是近似于 Gamma 函数。比如，sRGB 的实际转换函数为：

\[L = \begin{cases} {\alpha}\frac{V}{12.92}, & V \leq 0.04045 \\ {\alpha}\left( \frac{V + 0.055}{1.055} \right)^{2.4}, & V > 0.04045 \end{cases}\]

向下兼容

看起来，HDR 和 SDR 并没有什么本质区别，无非是 HDR 选择了一个色域更大的色彩空间，HDR 显示设备能支持更高的亮度罢了。其实不然，我们还有一些问题尚未解决，

色彩空间的描述与转换

我们先来聊聊那些还没迈入 HDR 时代就需要思考的问题。怎么描述一个图片、视频、显示器或打印机所使用的色彩空间？不同的色彩空间之间又是如何进行转换的？

1994 年，国际色彩联盟（International Color Consortium，ICC）制定了 ICC 特性文件（ICC Profile）规范，用于在计算机系统中描述色彩输入、输出设备或色彩空间的特性。

在色彩空间转换，比如在以 sRGB 色彩空间显示的显示器上观看 Adobe RGB 色彩空间记录的图像时，系统会将图像的色彩信号从 Adobe RGB 色彩空间转换到一个公共的色彩空间，这个空间称为特性文件连接空间（Profile Connection Space，PCS），前面我们提过的 CIE 1931 XYZ 色彩空间就是其中一种 PCS，之后再将 PCS 的色彩信号转换到 sRGB 色彩空间进行显示。

系统会根据 ICC 特性文件中所记录的转换意图（Rendering Intent）来决定色彩如何映射：

  • 相对色度意图（Media-relative Colorimetric Intent），将源色彩空间（上文例子中图像的 Adobe RGB）中落在目标色彩空间（上文例子中显示器的 sRGB）色域之外的颜色映射到目标色彩空间中最接近的颜色，保持色彩的相对关系，但可能会导致超出目标色彩空间的部分颜色在映射后失真。
  • 绝对色度意图（ICC-absolute Colorimetric Intent），与媒体相对色度意图类似，但会使用源色彩空间的白点，一般用于打印。
  • 感知意图（Perceptual Intent），将源色彩空间缩限或扩展到目标色彩空间的色域范围内，尽量保证灰度平衡，但不保证颜色之间的相对关系，一般用于显示图像。
  • 饱和度意图（Saturation Intent），优先保持颜色的饱和度，适用于商业图形设计等对色彩鲜艳度要求较高的场景，但可能会导致颜色失真。

位深

根据前文的内容，我们可以了解两个事实：

  • 对于 RGB 色彩模型来说，色彩本质上是由三个基色的亮度决定的。
  • 在计算机领域，连续的亮度值通常会被量化为离散的整型数据进行存储与处理，这些整数所能表现的亮度数量是有限的。

这两个事实决定了，计算机无法表示色彩空间内无限的颜色，只能通过整型数据来表示色彩空间中有限个离散的点，整型的宽度决定了整型的取值范围，也间接决定了所能表示的颜色数量，单个基色所使用的整型宽度称为位深（Bit Depth），而表示色彩所使用的整型宽度称为色深（Color Depth，对于 RGB 色彩模型来说，色深是三个基色的位深之和，也就是位深的三倍）。通常我们所见到的像 #FFFFFF 这样表示的颜色值，就使用目前最常见的 8bit 位深，或称 24bit 色深。

#FFFFFF 是 16 进制表示的颜色值，每两个字符表示一个 8bit 的整型，正好是一个 byte 的大小。这三个 byte 按顺序分别对应 RGB 三个基色的信号数据。

比如 #ABCDEF 中，红、绿、蓝三个基色的信号值分别为 0xAB（171）、0xCD（205）、0xEF（239）。

对于 HDR 来说，它所使用的色彩空间比 SDR 更大，但如果仍然用 8bit 位深来表示颜色，那没有对可表示色彩数量进行任何改变，反而因为色彩空间变大，量化后的离散点变得更加稀疏。因此，HDR 通常需要使用更高的位深来表示颜色，比如 10bit 或 12bit。

由于幂指数增长的特性，虽然 8bit 提升到 10bit 只增加了 2bit，但可表示的颜色数量从 \((2^8)^3 = 16,777,216\) 提升至 \((2^{10})^3 = 1,073,741,824\)，后者等于前者的 64 倍。

PQ 与 HLG

接下来就要面临通往 HDR 最大的挑战了 —— 亮度。

我们重新来看一下 HDR 这个词。高动态范围（High Dynamic Range，HDR）中的 “动态范围（Dynamic Range）” 一词，是信号领域表示最小值与最大值之间比率的术语，通常使用分贝（Decibel，符号为 dB）来表示，但在摄影领域通常采用挡（Stop）作为亮度动态范围单位，每提升一挡，后者的值是前者的两倍。

举些例子，人眼的亮度动态范围大约在 20 挡以上，而大部分 SDR 内容的亮度动态范围通常在 6~10 挡左右，HDR 内容的亮度动态范围通常在 10~14 挡左右。一些如 OLED 等显示方案的显示器在显示黑色时能完全关闭像素，因此它们的理论亮度动态范围为无限，即使峰值亮度有限，相比普通的高亮 LED 显示器也能有更佳的显示表现。不过，受限于环境光照等条件，常见提升动态范围的方法还是提升峰值亮度。

SDR 内容的峰值亮度通常在 100 cd/m² 左右，而 HDR 根据不同的标准，峰值亮度一般远大于 100 cd/m²，比如 1000 cd/m² 甚至更高，高于 SDR 峰值亮度的部分称为余量（Headroom）。不同 HDR 标准、内容或显示设备的余量是不同的，这种 “几乎” 没有上限的特性，决定了不同 HDR 内容在不同 HDR 显示设备上的显示效果可能有很大的差异。如果我们的 HDR 内容要兼容更小范围的 HDR 显示设备，甚至 SDR 显示设备，即便无法呈现原本内容的视觉效果，也至少要保证内容的正确表达，此时我们会面临两个问题：

  • 如果武断裁切余量，那么内容的高光细节会全部丢失，除非显示设备的显示余量足够大，否则显示效果就会变成一片死白。
  • 如果将 HDR 内容线性映射到显示设备的亮度范围内，非高亮的内容通常占据了大部分的内容比重，那么在低峰值亮度的显示设备上观看时，低亮度区域的细节会被压缩，导致画面整体偏暗。

Dolby 和电影电视工程师协会（Society of Motion Picture and Television Engineers，SMPTE）整了一个某种意义上算是破罐子破摔的方案，就是创建了一个称为感知量化（Perceptual Quantizer，PQ）的转换函数。PQ 由 Dolby 开发，并在 2014 年被 SMPTE 标准化为 SMPTE ST 2084，定义了信号值与实际亮度之间的绝对映射关系，函数定义如下：

\[L = 10000 \left( \frac{\max\left[ V^{1/m_2} - c_1, 0 \right]}{c_2 - c_3V^{1/m_2}} \right)^{1/m_1} \quad \begin{array}{l} m_1 = \frac{2610}{16384} = 0.1593017578125 \\ m_2 = \frac{2523}{32} = 78.84375 \\ c_1 = \frac{3424}{4096} = 0.835937 \\ c_2 = \frac{2413}{128} = 18.8515625 \\ c_3 = \frac{2392}{128} = 18.6875 \\ \end{array}\]

\(L\) 取值为 \([0, 10000]\)，基本完全覆盖了人眼在单一场景中能有效感知的亮度范围。

配合 PQ，我们需要一个新的东西来实现对目标设备的亮度映射，否则就会面临刚才提出两个问题中的第二个：低亮度区域的细节会被压缩，导致画面整体偏暗，对于能记录 0~10000 cd/m² 如此广亮度范围的 PQ 来说，问题尤为严重。这个东西称为元数据（Metadata），用于描述内容的亮度范围信息，从而帮助显示设备忽略没有被使用的亮度范围，从而根据内容的实际亮度范围来完成映射。比如元数据中记录了内容仅使用了 100~400 cd/m² 亮度范围，那么显示设备就可以将这个范围映射到自身的亮度范围内，而不是映射整个 0~10000 cd/m² 亮度范围。

PQ 的 EOTF 函数图像

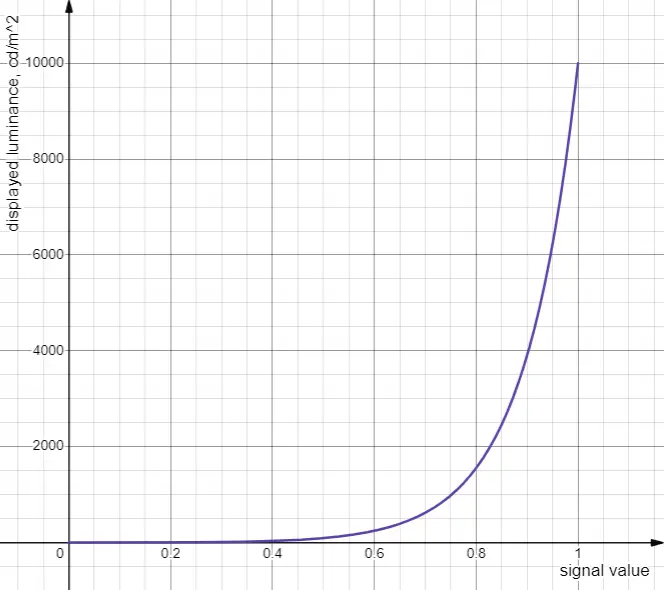
以视频领域的 HDR10 标准为例，HDR10 定义了两种元数据：内容最高亮度（Maximum Content Light Level，MaxCLL）与帧内最高平均亮度（Maximum Frame Average Light Level，MaxFALL），分别表示视频内容中所出现的最高亮度，和视频内容中帧序列里最高的帧平均亮度。

除此之外，对于上述这种整个视频仅定义单一元数据的方式，称为静态元数据（Static Metadata），而如 HDR 10+ 或 Dolby Vision 等则使用了动态元数据（Dynamic Metadata），元数据会随帧序列动态变化，从而避免高亮帧与低亮帧显示效果差距过大的问题。

另一个常见于 HDR 的转换函数是英国广播公司（British Broadcasting Corporation，BBC）与日本广播协会（日本(Nippon)放送(Hoso)協会(Kyokai)，NHK）联合开发的混合对数伽马（Hybrid Log-Gamma，HLG），函数定义如下：

\[\begin{array}{l} D = OETF[E] = \begin{cases} \sqrt{3E}, & 0 \leq E \leq \frac{1}{12} \\ a \ln{(12E - b)} + c, & \frac{1}{12} < E \leq 1 \end{cases} \\ L = OOTF[E] = \alpha Y_S^{\gamma - 1} E \\ L = EOTF[D] = OOTF[OETF^{-1}[max(0, (1 - \sqrt{3(\frac{L_B}{L_W})^{\frac{1}{\gamma}}}) + \sqrt{3(\frac{L_B}{L_W})^{\frac{1}{\gamma}}})]] \end{array}\]

其中，常量：

\[\begin{array}{l} a = 0.17883277 \\ b = 1 - 4a = 0.28466892 \\ c = 0.5 - a \ln{(4a)} = 0.55991073 \\ \end{array}\]

变量 \(Y_S\) 为归一化后的场景亮度，\(\alpha\) 为用户增益，\(\gamma\) 为显示设备 Gamma，\(L_B\) 为显示设备的黑电平亮度，\(L_W\) 为显示设备的白点亮度。

函数很复杂，但总结一下具体的表现结果是，HLG 在低亮度区域的非常接近与传统的 Gamma 函数，而高亮度区域采用对数函数来记录更高的亮度范围，对于 SDR 显示设备来说，通过 HLG 记录的亮度信号值，换用传统的 Gamma 函数进行显示也能获得不错的效果，因此 HLG 有着非常好的向下兼容性。

HLG 与 Gamma 的函数图像对比

CICP

这里再额外介绍一个与 ICC 特性文件职能类似的标准 —— 编码独立代码点（Coding-Independence Code Points，CICP），它在 ITU-T H.273 与 ISO/IEC 23091-2 中被定义。CICP 最初用于视频编码领域，相比 ICC 特性文件，CICP 仅使用几个整数值来描述色彩空间的各个属性，这些整数通过查表的方式获得其在标准中的具体定义。CICP 与 HDR 有关的几个主要属性如下：

  • 色彩原色（Color Primaries），与上文提到的色彩原色概念一致。比如 sRGB 对应的值为 1，Rec. 2020 对应的值为 9。
  • 转换特征（Transfer Characteristics），与上文提到的转换函数概念一致。比如 sRGB 对应的值为 13，Rec. 709 对应的值为 1，PQ 对应的值为 16，HLG 对应的值为 18。
  • 矩阵系数（Matrix Coefficients），用于描述色彩模型的转换矩阵，比如 YCbCr 与 RGB 之间的转换。对于 RGB 色彩模型来说，对应的转换矩阵为单位矩阵，其值为 0。

HDR 目前在图像领域的应用

在啰嗦了这么多内容之后，我们终于可以回到最初的话题了 —— HDR 在图像领域的应用。相比视频领域，图像的应用场景更加多样，因此兼容性要求更高，基本要求 HDR 对 SDR 完全兼容。

目前 HDR 图像主要采用以下两种方案实现。

原生数据记录

一种是使用更高位深、更广色域色彩空间来记录、使用 HLG 或 PQ + Metadata 来兼容不同显示设备的 “原生” 方案。2023 年 6 月，由 Apple 与 Adobe 合作发布的 ISO/TS 22028-5:2023 确定了 HDR 静态图像的编码标准。

近期 PNG 3.0 所采用的 HDR 标准也属于这一类。PNG 新增了 cICP 数据块标准，用于记录四个 CICP 属性，除了上文所提到的色彩原色、转换特征与矩阵系数之外，还额外记录了一个称为视频全范围标记（Video Full Range Flag）的属性，对于常见用完整位深整数表示亮度的图像（也被称为全范围图像，Full-Range Image），此值为 1。

在 PNG 中，可选的数据块以小写字母开头，解码器可以选择性地忽略这些数据块。

在视频全范围标记这个属性上，对应地，如果此值为 1，则表示图像是窄范围图像（Narrow-Range Image），常见于视频工作流程，其亮度值并不使用完整的整数范围进行表示。例如，在 ITU-R-BT.709 标准的 10bit 编码中，黑色对应的信号值为 64，白色对应的信号值为 940，而不是 0 与 1023，目的是保留冗余空间，从而避免因滤波或压缩导致的亮度裁切。

Gain Map

另一种方案使用了一种称为增益图（Gain Map）的额外数据。

增益图的本质是是一张或多张灰度图像，以蒙版的形式记录 HDR 图像与 SDR 图像之间的亮度差异信息。对于 SDR 显示设备来说，仅需忽略增益图，直接显示 SDR 图像即可，而对于 HDR 显示设备来说，则可以通过增益图对 SDR 图像进行亮度增强，从而获得更高的亮度范围与更丰富的细节表现。

如果不考虑色彩断层等问题，增益图甚至可以用于 8bit 位深图像，这意味着 JPEG 等传统图像格式也能用增益图实现 HDR 显示效果。

2025 年 7 月，ISO 发布了 ISO 21496-1:2025 标准，定义了增益图的技术标准。

Apple 在 WWDC 2024 上展示的增益图实现示意

参考资料